La explicación "divulgativa" tradicional del
principio de incertidumbre afirma que las variables dinámicas como posición,
momento angular, momento lineal, etc. se definen de manera operacional, esto
es, en términos relativos al procedimiento experimental por medio del cual son
medidas: la posición se definirá con respecto a un sistema de referencia
determinado, definiendo el instrumento de medida empleado y el modo en que tal
instrumento se usa (por ejemplo, midiendo con una regla la distancia que hay de
tal punto a la referencias ).
Sin embargo, cuando se examinan los procedimientos
experimentales por medio de los cuales podrían medirse tales variables en
microfísica, resulta que la medida siempre acabará perturbada por el propio
sistema de medición. En efecto, si por ejemplo pensamos en lo que sería la
medida de la posición y velocidad de un electrón, para realizar la medida (para
poder "ver" de algún modo el electrón) es necesario que un fotón de
luz choque con el electrón, con lo cual está modificando su posición y
velocidad; es decir, por el mismo hecho de realizar la medida, el
experimentador modifica los datos de algún modo, introduciendo un error que es
imposible de reducir a cero, por muy perfectos que sean nuestros instrumentos.
Esta descripción cualitativa del principio, sin ser
totalmente incorrecta, es engañosa en tanto que omite el principal aspecto del
principio de incertidumbre: el principio de incertidumbre establece un límite
más allá del cuál los conceptos de la física clásica no se pueden emplear. La
física clásica concibe sistemas físicos descritos por medio de variables
perfectamente definidas en el tiempo
(velocidad, posición,...) y que en
principio pueden conocerse con la precisión que se desee. Aunque en la práctica
resultara imposible determinar la posición de una partícula con una precisión
infinitesimal, la física clásica concibe tal precisión como alcanzable: es
posible y perfectamente concebible afirmar que tal o cual partícula, en el
instante de tiempo exacto 2 s, estaba en la posición exacta 1,57 m. En cambio, el
principio de incertidumbre, al afirmar que existe un límite fundamental a la
precisión de la medida, en realidad está indicando que si un sistema físico
real se describe en términos de la física clásica, entonces se está haciendo
una aproximación, y la relación de incertidumbre nos indica la calidad de esa
aproximación.
Por motivos culturales y educativos, las personas se suelen
enfrentar al principio de incertidumbre por primera vez estando condicionadas por
el determinismo de la física clásica. En ella, la posición x de una partícula
puede ser definida como una función continua en el tiempo, x=x(t). Si la masa
de esa partícula es m y se mueve a velocidades suficientemente inferiores a la
de la luz, entonces el momento lineal de la partícula se define como masa por
velocidad, siendo la velocidad la primera derivada en el tiempo de la
posición: p=m \frac{dx}{dt}.
Dicho esto, atendiendo a la explicación habitual del
principio de incertidumbre, podría resultar tentador creer que la relación de
incertidumbre simplemente establece una limitación sobre nuestra capacidad de
medida que nos impide conocer con precisión arbitraria la posición inicial x(0) y
el momento lineal inicial p(0) . Ocurre que si pudiéramos conocer x(0)
y p(0) , entonces la física clásica nos ofrecería la
posición y la velocidad de la partícula en cualquier otro instante; la solución
general de las ecuaciones de movimiento dependerá invariablemente de x(0) y
p(0) . Esto es, resolver las
ecuaciones del movimiento lleva a una familia o conjunto de trayectorias
dependientes de x(0) y
p(0) ; según qué valor tomen x(0)
y p(0) , se tendrá una trayectoria dentro de esa
familia u otra, pero la propia resolución de las ecuaciones limita el número de
trayectorias a un conjunto determinado de ellas. Según se ha razonado, de
acuerdo con el principio de incertidumbre
x(0) y p(0) no
se pueden conocer exactamente, así que tampoco podrán conocerse x(t)
y p(t) en cualquier otro instante con una precisión
arbitraria, y la trayectoria que seguirá la partícula no podrá conocerse de
manera absolutamente exacta. Este razonamiento es, sin embargo, incorrecto,
pues en él subyace la idea de que, pese a que
x(0) y p(0)
no se pueden conocer exactamente, es posible continuar usando la descripción
clásica en virtud de la cual una partícula seguirá una trayectoria definida por
la solución general de las ecuaciones de movimiento, introduciendo la noción
añadida de que las condiciones iniciales
x(0) y p(0)
no pueden conocerse al detalle: esto es, no podemos conocer exactamente
qué trayectoria va a seguir la partícula, pero estaremos aceptando que, de
facto, va a seguir una.
Esta forma de proceder es, sin embargo, totalmente
incorrecta: el principio de incertidumbre conlleva un desvío completo de las
concepciones clásicas, haciendo que la noción clásica de trayectoria debe ser
desechada: preguntar cuáles son simultáneamente los valores de x(t) y p(t)
es un absurdo. Así dicho, podría resultar paradójico que primero se
establezca una relación de incertidumbre en términos de posición x y
momento lineal p , para luego afirmar que x
y p , que aparecen en dicha relación, no tienen
sentido: si no tienen sentido, ¿qué sentido puede tener una relación que las
emplee? Ocurre que, en física cuántica, es posible introducir una serie de
entidades matemáticas x y
p que se correspondan en muchos
aspectos con la posición y el momento clásicos. Dichas entidades no son, no
obstante, exactamente iguales a la posición y el momento clásicos: el principio
de incertidumbre sencillamente indica que si interpretamos esas entidades como
posición y momento lineal -y por tanto interpretamos el movimiento de una forma
clásica-, entonces existe un límite fundamental en la precisión con que dichas
variables pueden ser conocidas; esto es, si intentamos introducir variables
clásicas e intentamos interpretar el movimiento de forma clásica, la precisión
con que estas variables pueden ser especificadas está limitada.

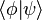
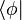


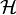
 para todos los kets
para todos los kets