La notación bra-ket, también conocida como notación de Dirac, es la notación estándar para describir los estados cuánticos en la teoría de la mecánica cuántica. Puede también ser utilizada para denotar vectores abstractos y funcionales lineales en las matemáticas puras. Es así llamada porque el producto interior de dos estados es denotado por el "paréntesis angular" (angle bracket, en inglés), 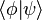 , consistiendo en una parte izquierda,
, consistiendo en una parte izquierda, 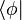 , llamada el bra, y una parte derecha,
, llamada el bra, y una parte derecha,  , llamada el ket.
, llamada el ket.
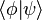 , consistiendo en una parte izquierda,
, consistiendo en una parte izquierda, 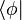 , llamada el bra, y una parte derecha,
, llamada el bra, y una parte derecha,  , llamada el ket.
, llamada el ket.
En mecánica cuántica, el estado de un sistema físico se identifica
con un vector en el espacio de Hilbert complejo, 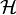 . Cada vector se llama unket, y se denota como
. Cada vector se llama unket, y se denota como  . Cada ket
. Cada ket  tiene un bra dual, escrito como
tiene un bra dual, escrito como 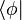 , esto es una funcional lineal continua de
, esto es una funcional lineal continua de 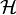 a los números complejos C, definido como
a los números complejos C, definido como
 |
| Paul Dirac |
 . Cada vector se llama unket, y se denota como
. Cada vector se llama unket, y se denota como  . Cada ket
. Cada ket  tiene un bra dual, escrito como
tiene un bra dual, escrito como 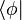 , esto es una funcional lineal continua de
, esto es una funcional lineal continua de 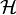 a los números complejos C, definido como
a los números complejos C, definido como para todos los kets
para todos los kets 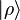
Donde () denota el producto interior definido en el espacio de Hilbert. La notación está justificada por el teorema de representación de Riesz, que establece que un espacio de Hilbert y su espacio dual son isométricamente isomorfos. Así, cada bra corresponde a exactamente un ket, y viceversa.
Incidentemente, la notación bra-ket puede ser utilizada incluso si el espacio vectorial no es un espacio de Hilbert. En cualquier espacio de Banach B, los vectores pueden ser notados como kets y los funcionales lineales continuos por los bras. Sobre cualquier espacio vectorial sin topología, se puede también denotar los vectores con kets y los funcionales lineales por los bras. En estos contextos más generales, el braketno tiene el significado de un producto interno, porque el teorema de representación de Riesz no se aplica.
La aplicación del bra 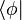 al ket
al ket  da lugar a un número complejo, que se denota:
da lugar a un número complejo, que se denota:
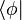 al ket
al ket  da lugar a un número complejo, que se denota:
da lugar a un número complejo, que se denota: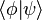 .
.
En mecánica cuántica, ésta es la amplitud de probabilidad para que el estado ψ colapse en el estado φ.
Texto extraído de: wikipedia.org
Un cordial saludo. Teniendo en cuenta el reconocimiento académico que ya están adquiriendo las respuestas emitidas por los Programas de Inteligencia Artificial en consultas sobre temas de Física, les cuento lo siguiente: se consultó a 7 programas de I.A. acerca de "la unidad de medida de la Constante de Planck" y TODOS coincidieron! en afirmar que "en base a conceptos básicos de la Física, en la unidad de medida de la Constante de Planck se encuentra implícito (es decir, conceptualmente su presencia es trivial pero que ha sido ignorado en el tratamiento académico de esta unidad de medida) un término en su denominador, y cuya presencia tiene notables implicaciones para la correcta interpretación de la naturaleza física de esta constante" (!?). Dado estos antecedentes, resulta evidente que el tema merece ser analizado seriamente pues se trata en este caso de "determinar si TODOS estos programas de I.A. se equivocaron en esta consulta"! (lo cual de por sí ya sería trascendente porque se estaría cuestionando la confiabilidad de estos programas!) o por el contrario "confirmando que que las respuestas son veraces"! Si les resulta de interés darle un "vistazo" hacédmelo saber a (diazreyesjosealberto62@gmail.com) para enviarles los textos. Atentamente, José Alberto
ResponderEliminar